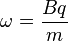Magnetyzm

Cyklotron — najprostsza i pierwsza historycznie forma akceleratora cyklicznego cząstek obdarzonych ładunkiem elektrycznym.

W akceleratorach cyklicznych, także w cyklotronie, przyspieszane cząstki poruszają się po torach zbliżonych do kołowych, przebiegając wielokrotnie przez obszar w którym są przyspieszane.

Historia

Pierwszy cyklotron zbudowano pod kierownictwem Ernesta Lawrence'a w University of California, w 1931 roku. Akcelerator był używany w eksperymentach nad zderzaniem cząstek jako źródło cząstek o energii do 1 MeV.

Obecnie cyklotrony są używane do:

wytwarzania wiązki cząstek o określonej wysokiej energii używanych głównie do prowadzenia badań podstawowych oraz wykorzystywanych praktycznie np. w leczeniu nowotworów,
uzyskiwania promieniowania rentgenowskiego o określonej częstotliwości w wyniku zjawiska promieniowania cyklotronowego,
produkcji izotopów o krótkim czasie połowicznego rozpadu używanych w PET
selekcjonowania cząstek w spektrometrach masy.

Pierwszy polski cyklotron uruchomiono w podkrakowskich Bronowicach 22 listopada 1958 roku. Obecnie w Polsce działają cyklotrony w Krakowie, Warszawie i w Instytucie Problemów Jądrowych w Świerku pod Warszawą.

Zasada działania [edytuj]

Wiązka elektronów poruszających się po orbicie kołowej w stałym polu magnetycznym

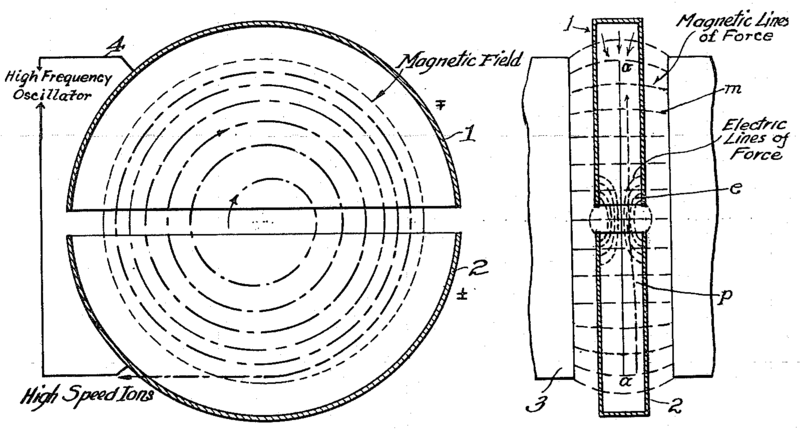
Cyklotron składa się z elektromagnesu wytwarzającego pole magnetyczne i komory próżniowej, w której umieszczono dwie półkoliste elektrody zwane duantami. Między elektrodami wytwarzane jest za pomocą generatora wysokiej częstotliwości zmienne pole elektryczne. W centrum cyklotronu znajduje się źródło cząstek (cząsteczek) naładowanych elektrycznie lub cząsteczki te są wprowadzane z zewnątrz. Jeżeli częstotliwość generatora jest równa częstotliwości obiegu cząstek, to są one przyspieszane podczas przelotu między duantami. Cząstki o innym czasie przelotu są okresowo przyspieszane i hamowane i w końcu uderzają w duanty. Cząsteczki o większej energii poruszają się po większym promieniu. Gdy promień toru ruchu cząstki jest odpowiednio duży, może ona opuścić akcelerator; pomocna w tym może być dodatkowa elektroda kierująca cząstki w odpowiednią stronę.

Częstotliwość cyklotronowa

Na cząstkę poruszającą się prostopadle do pola magnetycznego działa siła Lorentza prostopadła do wektorów prędkości i indukcji pola magnetycznego; siła ta pełni rolę siły dośrodkowej:

$\frac{mv^2}{r} = Bqv$

Gdzie m to masa cząstki, q jej ładunek, v prędkość, r to promień toru ruchu, B – indukcja pola magnetycznego.

Przekształcając,

$\frac{v}{r} = \frac{Bq}{m}$

v/r odpowiada prędkości kątowej ω, dlatego

$\omega = \frac{Bq}{m}$

Co odpowiada częstotliwości

$f = \frac{Bq}{2\pi m}$

Ze wzoru tego wynika, że częstotliwość rezonansowa nie jest zależna od prędkości cząstek, ale - przy stałym polu magnetycznym - zależy od stosunku ładunku do masy cząstki. Własność ta sprawia, że cyklotron przyspiesza tylko jeden rodzaj cząstek, co może być jego wadą, ale też zaletą. Cechę tę wykorzystuje się do separacji cząstek w analizatorach mas stosowanych w różnych spektrometrach masy.

Efekty relatywistyczne

Przyspieszając cząstki do prędkości porównywalnych z prędkością światła, napotyka się w cyklotronach problem relatywistycznego wzrostu masy przyspieszanej cząstki. Problem ten można rozwiązać, zmieniając częstotliwość prądu zasilającego duanty. Częstotliwość ta musi spełniać zależność:

$f=f_c\frac{m_0}{m_0+T/c^2}$ ,

gdzie $f c$ jest częstotliwością w przybliżeniu klasycznym, T – energią kinetyczną cząstki, $m 0$ – masą spoczynkową cząstki, c – prędkością światła.

Przy czym energia kinetyczna jest proporcjonalna do liczby przebiegów przyspieszanych cząstek między elektrodami – oznacza to, że jest proporcjonalna do czasu przyspieszania cząstek. Cyklotron przystosowany do odpowiedniej zmiany częstotliwości w miarę przyspieszania cząstek nosi nazwę synchrocyklotronu.

Innym urządzeniem jest synchrotron, w którym wzrost masy cząstki kompensuje się, zwiększając natężenie pola magnetycznego.

Modyfikacją w budowie cyklotronów są cyklotrony izochroniczne, w których efekty relatywistyczne są niwelowane przez modyfikację budowy elektromagnesu tak, by pole magnetyczne było tym silniejsze, im dalej od środka akceleratora.

Promieniowanie cyklotronowe

Cząstka naładowana, poruszając się w polu magnetycznym, wysyła promieniowanie zwane promieniowaniem cyklotronowym. Jego moc rośnie wprost proporcjonalnie do kwadratu prędkości przyspieszanych cząstek, co powoduje zmniejszenie ich energii. Moc tę wyraża wzór

$P={\sigma B^2 v^2 \over c \mu_o}$